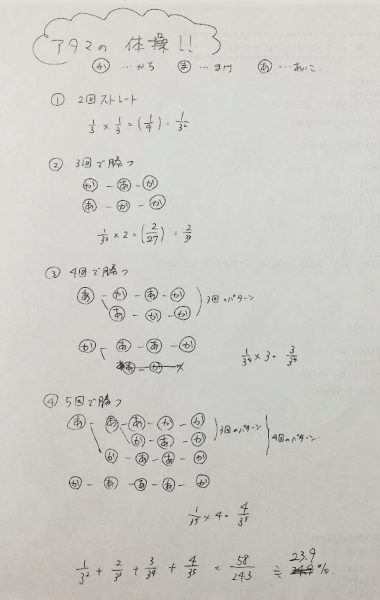ランチを食べていたら、「じゃんけんに勝つとワインボトルが無料に」というチラシが貼ってありました。
聞けば、1番上のボジョレーはじゃんけんに「2回」勝つとボトルが無料になるらしいです。
はて、「どれぐらいの確率で勝てるのか?」というのが議論になったので、久々に高校時代の宝刀「数学」を持ち出して真面目に計算してみました。
もくじ
じゃんけんで勝つ確率は・・・?
じゃんけんで勝つ確率は、1/3(三分の一)です。
計算では書いていませんが、2人でじゃんけんをする場合、パターンは3×3=9通りになります。
そして、勝てるパターンというのがグーチョキパーそれぞれについて1通りずつあるので、勝てる確率としては3/9=1/3となるわけです。
ただ、今回のじゃんけんの場合はあいこがないので、「勝ち」「負け」の実質1/2になると考えられます(仮説)。
となると、2回勝つ確率は単純に考えると1/2×1/2で1/4(25%)になるんじゃないのかな?というのが今回の検証の始まりです。
実際に計算してみた
実際に書き出してみました。ただ、数学をやるのは大学受験以来なので、間違ってたらごめんなさい(^^;)
試行回数が決まっていれば簡単に計算できますが、今回の場合永遠にあいこという可能性もゼロではないので、ひたすら書き出すしかありません。
ただし、5回で勝つ確率までを考えたときにすでに23.9%なので、仮説は正しかったと考えられます。
画像をご覧頂くとわかるのですが・・・あ、私の字が汚いというのはもはや触れません(^^;)
どうやら○回で勝つ確率には法則がありそうです。
たとえば、4回で勝つパターンは、1回目が勝ちだった場合は、3回で勝つパターンの回数分だけ勝ち方があり、それに最初が勝ちだったときの新パターンが1つ加わったものになっています。
そこで、考えたのが、次の仮説です。
n≧2以上の時、メモにある一般式が成り立つと考えられます。
その場合、この勝負に勝てる確率を計算しようと思うと、上記の極限式になるのではないかと思います。
が、計算がめんどくさかったので、n=10までで計算してみると24.9911%でした。やはり25%に収束すると考えられます。
まとめ
じゃんけんで2回勝てば無料になるといったケースでは、25%の確率で勝つことが可能です。
やる側としてもリスクはないですし、お店側にとっても良い条件だと言えます。仮にお店が負けたとしても、原価はもっと低いはずですし、その分おつまみの消費も期待できますしね。
こんな会話をしていたのですが、会計時に店員さんには、『じゃんけんしに来てくださいね♪』と一言だけ声をかけられたとさ(^^;)
 薬機法コピーライティング®ならB&H Promoter'sへ
薬機法コピーライティング®ならB&H Promoter'sへ